Cet article explique comment sélectionner un transformateur – une étape cruciale dans la conception d’un convertisseur buck isolé – en incluant les paramètres à prendre en compte, les calculs à suivre et comment ces paramètres influencent le circuit global.
Cet article est publié par pÉlectrique dans le cadre d’un partenariat de contenu numérique exclusif avec Bodo’s Power Systems.
Cet article explique le fonctionnement d’un convertisseur buck isolé et comment sélectionner un transformateur – une partie cruciale de la conception d’un convertisseur buck isolé. Il discute des paramètres à prendre en compte, des calculs à suivre lors du choix d’un transformateur et de la façon dont ils influencent le circuit global.
Image utilisée avec l’aimable autorisation de Adobe Stock
Comment fonctionne un convertisseur buck isolé?
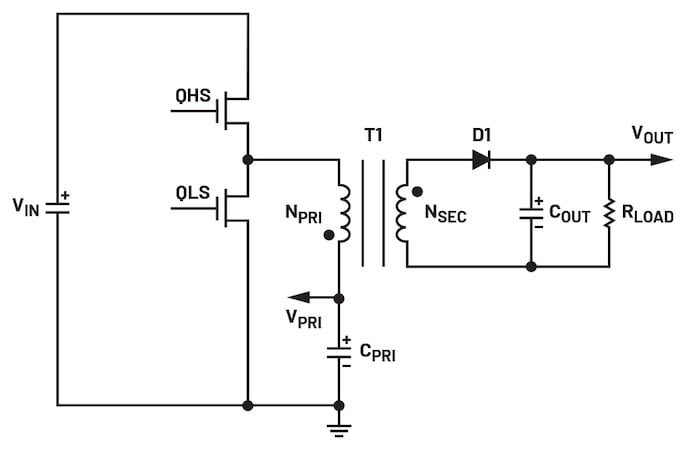
Une topologie buck isolée, comme illustré dans la Figure 1, est similaire à un convertisseur buck générique. Remplacer l’inductance dans un circuit buck par un transformateur donne un convertisseur buck isolé. Le côté secondaire du transformateur a une mise à la terre indépendante.
Figure 1. Une topologie buck isolée. Image utilisée avec l’aimable autorisation de Bodo’s Power Systems [PDF]
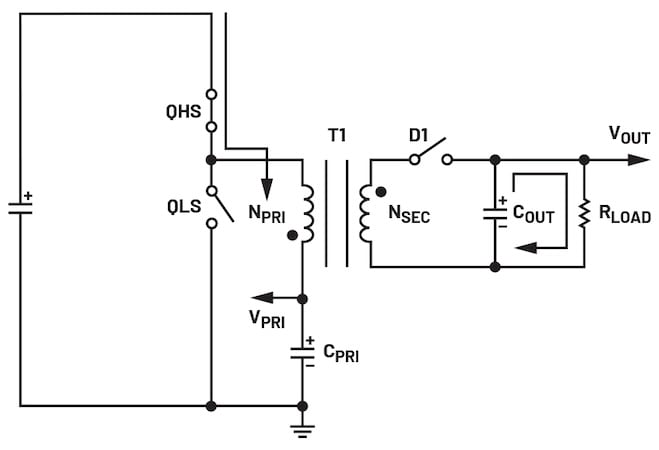
L’interrupteur du côté haute tension (QHS) est activé pendant le temps d’allumage, et l’interrupteur du côté basse tension (QLS) est éteint. L’inductance de magnétisation du transformateur (LPRI) se charge. Les flèches dans la Figure 2 montrent la direction du courant. Le courant primaire augmente de manière linéaire. La pente du courant dépend de (VIN – VPRI) et LPRI. La diode du côté secondaire, D1, est bloquée en inverse pendant cet intervalle de temps et charge le courant provenant de COUT jusqu’à la charge.
Figure 2. Circuit équivalent de la période d’allumage. Image utilisée avec l’aimable autorisation de Bodo’s Power Systems [PDF]
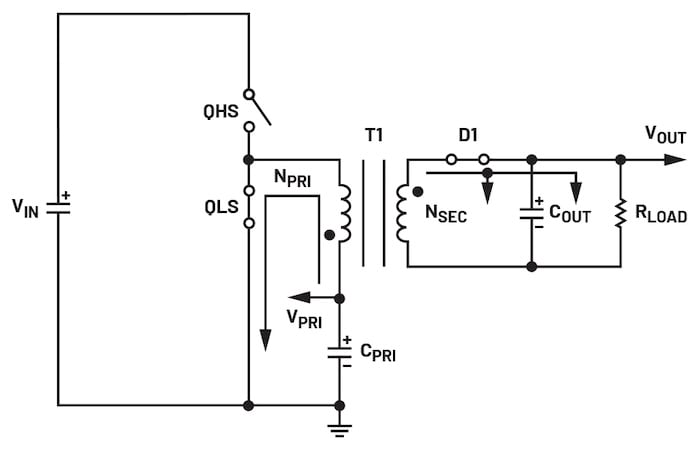
Pendant la période d’extinction, QHS est éteint, et QLS est allumé. L’inductance primaire se décharge. Le courant primaire circule de QLS à la terre, D1 est polarisé en direct, et le courant secondaire circule de la bobine du deuxième côté vers COUT et vers la charge. COUT se charge pendant cette période. (Éteindre QHS et allumer QLS ne peut pas changer la direction du courant ; cela ne peut que changer la pente du courant. Le courant positif diminue jusqu’à 0 A, puis le courant négatif augmente.)
Figure 3. Circuit équivalent de la période d’extinction. Image utilisée avec l’aimable autorisation de Bodo’s Power Systems [PDF]
Quelles spécifications influencent le transformateur?
Certaines spécifications doivent être déclarées et clarifiées lors de la conception d’un convertisseur. Cela déterminera quel composant sera utilisé, en particulier lors du choix d’un transformateur.
- Plage de tension d’entrée
- Tension de sortie
- Cycle de travail maximal
- Fréquence de commutation
- Ripple de tension de sortie
- Courant de sortie
- Puissance de sortie
Le cycle de travail maximal (D) est généralement compris entre 0,4 et 0,6. La tension d’entrée minimale (VIN_MIN) et le cycle de travail maximal détermineront la tension de sortie primaire (VPRI). Ensuite, la tension de sortie primaire (VPRI) et la tension de sortie secondaire (VOUT) détermineront le rapport de transformation du transformateur.
Le courant de sortie (IOUT) et la puissance de sortie (POUT) sont des paramètres clés qui influencent la sélection du transformateur. Le courant de sortie détermine l’épaisseur du fil de cuivre, tandis que la puissance de sortie détermine quelle bobine de transformateur doit être utilisée. La perméabilité de la bobine montre combien d’énergie elle peut stocker et quelle puissance elle peut délivrer. Généralement, le courant de sortie DC multiplié par un coefficient est assigné comme courant résiduel de l’inductance (transformateur). Le cycle de travail et la fréquence de commutation sont utilisés pour calculer le temps TON, tandis que VIN, VPRI et le courant résiduel déterminent l’inductance primaire. Le coefficient assigné ne doit pas être trop grand ou trop petit car un grand coefficient peut entraîner un grand courant résiduel. Un grand courant résiduel peut atteindre la moitié de la limite de courant du pont en H et endommager le MOSFET. Cela entraînera une grande tension résiduelle sur le condensateur de sortie en raison de sa RSE et de son ESL.
En revanche, lorsqu’un courant résiduel extrêmement faible est nécessaire, nous devons utiliser une inductance de valeur élevée (transformateur). Si la bobine a de nombreux tours, cela nécessitera une bobine volumineuse. La grande inductance limitera la bande passante en boucle et réduira l’indice de réponse dynamique.
Choisir un transformateur
L’énergie est transmise à la bobine secondaire uniquement pendant le temps TOFF. Le rapport de tours peut être déterminé par l’Équation 1 :
\[\frac{V_{OUT} + V_{D}}{V_{PRI}} = \frac{N_{SEC}}{N_{PRI}}\,\,\,(1)\]
Où VD est la tension de polarisation directe de la diode secondaire. Pour VPRI, nous assignons généralement un cycle de travail maximal de 0,4 à 0,6. La VPRI peut être calculée en utilisant l’Équation 2 :
\[V_{PRI} = D \times V_{IN\_MIN}\,\,\,(2)\]
Où D est le cycle de travail maximal, et VIN_MIN est la tension d’entrée minimale. À partir de l’Équation 2, nous pouvons calculer le rapport de tours. Dans un convertisseur buck non isolé, le courant résiduel est le même des deux côtés de l’inductance. Nous pouvons facilement calculer l’inductance requise en utilisant l’Équation 3.
\[L = \frac{(V_{IN\_MIN} – V_{OUT}) \times D}{f \times \Delta I}\,\,\,(3)\]
Où f est la fréquence de commutation, et ΔI est le courant résiduel. Comme discuté précédemment, le courant résiduel équivaut au courant de sortie DC multiplié par un coefficient :
\[\Delta I_{OUT} \times K\,\,\,(4)\]
Où K est le coefficient. Mais dans une topologie de convertisseur buck isolé, il y a un transformateur et non une inductance. Comment faire face à cela quand le composant est un transformateur plutôt qu’une inductance? Comme nous le savons, le rapport de courant équivaut à l’inverse du rapport de tours :
\[IPRI_{TOFF} = I_{SEC} \times \frac{N_{SEC}}{N_{PRI}}\,\,\,(5)\]
Où IPRITOFF est le courant secondaire converti en courant primaire en temps TOFF. Nous devrions ajouter un courant à deux bobines du transformateur comme courant équivalent à l’inductance.
\[ILeq = I_{PRI} + I_{SEC} \times \frac{N_{SEC}}{N_{PRI}}\,\,\,(6)\]
Figure 4. Un circuit typique MAX17682 dans EE-Sim OASIS, alimenté par SIMetrix/SIMPLIS. Image utilisée avec l’aimable autorisation de Bodo’s Power Systems [PDF]
Where ILeq est le courant équivalent à l’inductance. Si le transformateur a trois bobines supplémentaires, alors
\[ILeq = I_{PRI} + I_{SEC} \times \frac{N_{SEC}}{N_{PRI}} + I_{THI} \times \frac{N_{THI}}{N_{PRI}} + \cdot\cdot\cdot\,\,\,(7)\]
Est-ce correct? Voyons un résultat de simulation basé sur le MAX17682. La Figure 4 montre un circuit MAX17682, qui a été dessiné dans EE-Sim® OASIS, alimenté par SIMetrix/SIMPLIS. Des sondes de courant, étiquetées IPRI et ISEC1, ont été placées des deux côtés du transformateur.
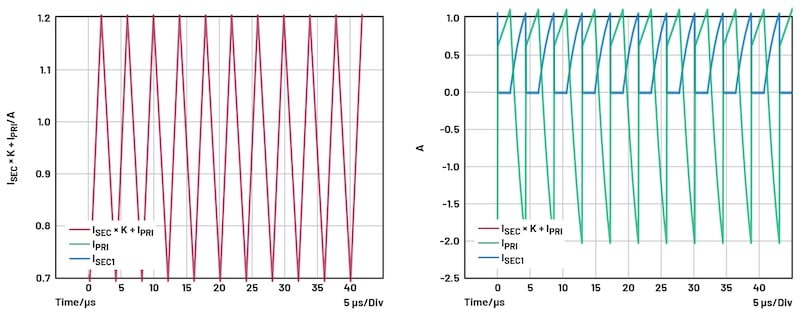
La Figure 5 montre un résultat de simulation transitoire des deux sondes de courant. Les deux formes d’ondes de courant ont été ajoutées en utilisant l’Équation 6.
Les résultats de courant ajoutés (rouge) dans une onde triangulaire se comportent comme l’inductance dans un convertisseur buck non isolé. Ainsi, le ΔI primaire du transformateur peut être facilement calculé :
\[\Delta I = (I_{PRI} + I_{SEC} \times \frac{N_{SEC}}{N_{PRI}}) \times K\,\,\,(8)\]
En général, nous assignons un courant résiduel de charge qui est 0.2 fois le courant de sortie DC. Ainsi, K peut être assigné à 0.2 fois NSEC/NPRI. En même temps, le courant de crête primaire devrait être conçu inférieur à la limitation de courant de l’interrupteur, où IPK est :
\[I_{PK} = ILeq_{DC} + \frac{\Delta I}{2}\,\,\,(9)\]
Ensuite, l’inductance primaire du transformateur peut être facilement calculée :
\[L_{PRI} = \frac{(V_{IN\_MIN} – V_{PRI}) \times D}{f \times \Delta I}\,\,\,(10)\]
En utilisant le rapport de tours, l’inductance primaire, la puissance de sortie, le courant de sortie et la tension d’isolation, nous pouvons décider quel inducteur sera utilisé ou conçu.
Pourquoi une équation simplifiée peut fonctionner
Voyons comment nous pouvons mieux comprendre et appliquer l’équation présentée dans la fiche technique du MAX17682 (voir Figure 6).
Conformément à la discussion précédente, l’Équation 10 peut être réécrite pour suivre l’Équation 11 pour le temps TOFF.
\[L_{PRI} = \frac{V_{PRI} \times (1 – D)}{f \times \Delta I}\,\,\,(11)\]
Figure 5. Un résultat de simulation de forme d’ondes de courant d’un circuit typique MAX17682. Image utilisée avec l’aimable autorisation de Bodo’s Power Systems [PDF]
Figure 6. Une capture d’écran de la fiche technique du MAX17682. Image utilisée avec l’aimable autorisation de Bodo’s Power Systems [PDF]
En supposant que D est de 0.6, si et seulement si ΔI était de 0.4 A, le polynôme (1 – D) et ΔI peuvent être réduits. Ensuite, l’Équation 11 et l’équation de la Figure 6 sont les mêmes. L’équation dans la fiche technique sélectionne déjà le courant résiduel primaire. Si nous assignons D comme 0.6, le courant résiduel primaire est de 0.4 A. En quantité, le cycle de travail TOFF équivaut au courant résiduel primaire.
\[\Delta = 1 – D\,\,\,(12)\]
Assurer une conception plus rapide
En utilisant l’équation simplifiée présentée dans la Figure 6, l’utilisateur assure une conception plus rapide avec un courant résiduel primaire équivalent au cycle de travail TOFF. Si vous souhaitez modifier le courant résiduel primaire ou utiliser un autre paramètre, suivez ce tutoriel.